发布时间:2023-01-30 10:38来源:www.sf1369.com作者:宇宇
内容提要:【矩阵乘以转置矩阵】热度:85
a的转置乘以a一般情况下不等于a乘a的转置,只有当a为对称矩阵时a的转置乘以a等于a乘a的转置。
扩展知识
将矩阵的行列互换得到的新矩阵称为转置矩阵,转置矩阵的行列式不变。如果n阶方阵a和它的转置相等 ,即a'=a,则称矩阵a为对称矩阵。
如果a'=-a,则称矩阵a为反对称矩阵。
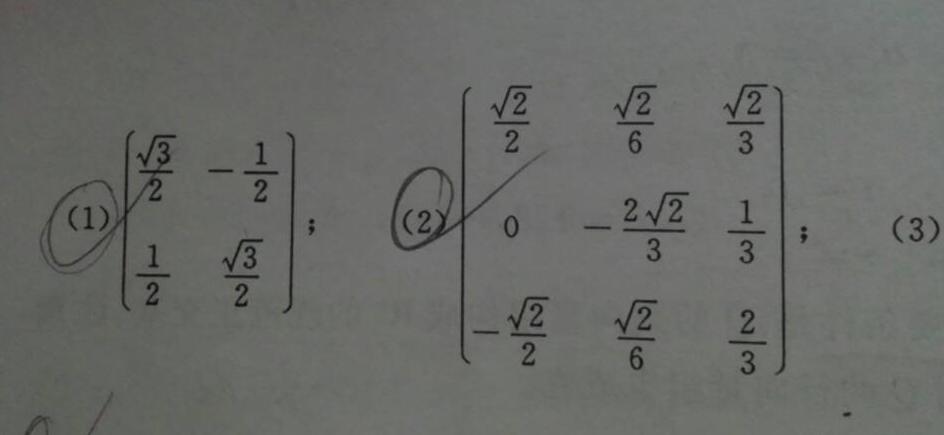
这是正交矩阵的定义。该矩阵每列元素做成向量,都是单位向量,且列向量组之间是正交的,因此列向量组是一个正交单位向理组。同样的,行向量组也是正交单位向量组。矩阵的行列式只能是1或-1。其逆矩阵就是它的转置矩阵。
这里e应该是一个列向量 至于求导, 就是一般的二次函数求(偏)导 d(e^T*J*e)/de=(J+J^T)e=2Je 至于导数写成行向量还是列向量很多情况下是无关紧要的, 关键看怎么用
等于,因为他的逆也是对称矩阵,注意到转置和逆是可交换的,也就是(A^-1)^T=(A^T)^(-1),因为A是对称的,故(A^-1)^T=A^(-1)得证。
实对称矩阵A的不同特征值对应的特征向量是正交的。实对称矩阵A的特征值都是实数,特征向量都是实向量。n阶实对称矩阵A必可对角化,且相似对角阵上的元素即为矩阵本身特征值。
Ax=0自然有A*Ax=0,而A*Ax=0意味着(x,A*Ax)=0即(Ax,Ax)=0即Ax=0。所以A与A*A核空间相同,所以秩相等
矩阵转置公式:(A^T)^T=A,(A+B)^T = A^T + B^T,(AB)^T = B^T*A^T。矩阵是一个按照长方阵列排列的复数或实数集合,最早来自于方程组的系数及常数所构成的方阵。矩阵是高等代数学中的常见工具,也常见于统计分析等应用数学学科中。
矩阵的运算是数值分析领域的重要问题。将矩阵分解为简单矩阵的组合可以在理论和实际应用上简化矩阵的运算。
最重要的一个公式,其余的每个都可以用这个来推导已知Y = AXB Y = A*X*BY=AXB那么有对X求导,公式(1)d Y d X = A TB T \frac{dY}{dX} = A^T*B^TdXdY=ATBT和对X T X^TXT求导,公式(2)d Y d X T = BA \frac{dY}{dX^T} = B*AdXTdY=BA下面我们来举例:
如果要计算Y = XB Y = X*BY=XB中,d Y d X \frac{dY}{dX}dXdY的值,我们可以令A = E A =EA=E代入公式(1),有d Y d X = B T \frac{dY}{dX} = B^TdXdY=BT其他计算同理。有一个小窍门,平时在推导的时候,可以根据矩阵的行列数来判断。具体的规律可以自己私下尝试
因为A乘A的秩等于A的秩,然后任意矩阵的转置矩阵的秩与原矩阵的秩相同。
A的秩 = A的行秩 = A的列秩,A^T 是 A 的行列互换,所以 r(A) = r(A^T)。矩阵的列秩和行秩总是相等的,因此它们可以简单地称作矩阵 A的秩。通常表示为 rk(A) 或 rank A。
1、设A为m*n的矩阵;
2、那么AX=0的解肯定是 AT*AX=0的解(AT表示A的转置);
3、至于AT*AX=0 左右两边乘以XT,(注意查看是否符合矩阵乘法,前后列行相等才能相乘);
4、上一步化成(AX)T*AX=0,可知AX=0,那么意味着AT*AX=0的解必定也是AX=0的解;
5、两个方程有相同的解,那么n-r(ATA)=n-r(A) 。
行列式转置前后值不变。
转置后行列式值不变,这是基本性质,与阶数无关。
行列式的基本性质:
转置后行列式值不变,这是基本性质,与阶数无关。
相等的,因为行列式最后是经过变换得到的,最后是用对角线上的乘积a的行变换和a转置矩阵的列变换得到的对角线是一样的值。
交换排列中两个元素的位置,改变排列的奇偶性,行列式的定义可改为按列标的自然序,正负号由行标排列的奇偶性决定。
总结:
1、用一个数k乘以向量a、b中之一的a,则平行四边形的面积就相应地增大了k倍。
2、把向量a、b中的一个乘以数k之后加到另一个上,则平行四边形的面积不变。
3、以单位向量(1,0),(0,1)构成的平行四边形(即单位正方形)的面积为1。
只有对称矩阵,反对称矩阵和正交矩阵满足矩阵的转置乘以矩阵等于矩阵乘以矩阵的转置。
如果矩阵不是方阵:
转置矩阵与原矩阵的乘积是一个方阵,阶数为原矩阵Amxn的列数n;原矩阵与转置矩阵的乘积是一个方阵,阶数为原矩阵的行数m。这两个矩阵不是同型矩阵,不相等。
扩展资料
如果矩阵是方阵:
(1)对称矩阵(转置矩阵=原矩阵)的转置矩阵与原矩阵的乘法满足交换律。
(2)反对称矩阵(转置矩阵=原矩阵的负矩阵)的转置矩阵与原矩阵的乘法满足交换律。
(3)正交矩阵(逆矩阵=转置矩阵)的转置矩阵与原矩阵的乘法满足交换律。
将矩阵的行列互换得到的`新矩阵称为转置矩阵,转置矩阵的行列式不变。
对称矩阵(Symmetric Matrices)是指元素以主对角线为对称轴对应相等的矩阵。在线性代数中,对称矩阵是一个方形矩阵,其转置矩阵和自身相等。
1.对于任何方形矩阵X,X+XT是对称矩阵。
2.A为方形矩阵是A为对称矩阵的必要条件。
3.对角矩阵都是对称矩阵。
4.两个对称矩阵的积是对称矩阵,当且仅当两者的乘法可交换。两个实对称矩阵乘法可交换当且仅当两者的特征空间相同。
秩是1。用A'表示A的转置,要证明r(A'A)=r(A),只需证明方程组AX=0和A'AX=0同解。
如果AX=0,两边分别左乘A',得A'AX=0,这说明方程组AX=0的解都是方程组A'AX=0的解;另一方面,如果A'AX=0,两边分别左乘X',得X'A'AX=0,即(AX)'AX=0,令Y=AX,则Y'Y=0,注意Y=AX为n维列向量,因此可设Y=(y1,y2,yn)',
则Y'Y=y1^2+...+yn^2=0,因此y1=yn=0,即Y=AX=0,这说明方程组A'AX=0的解都是方程组AX=0的解,综上我们证明了AX=0和A'AX=0同解,因此r(A'A)=r(A)。
只有矩阵为方阵时,才有对应的行列式的概念,一个转置矩阵如果有行列式,那么该的行列式的值与原矩阵的对应行列式的值是相等的,因为转自就是将矩阵的行与列对应变换,第一行的元素对应写到第一列对应位置,第二行的元素对应写到第二列对应位置,…,以此类推,所以它不改变行列式的大小